Concrete
Structure
Properties
Density : 2240 - 2400 kg/m3 (140 - 150 lb/ft3)
Compressive strength : 20 - 40 MPa (3000 - 6000 psi)
Flexural strength : 3 - 5 MPa (400 - 700 psi)
Tensile strength : 2 - 5 MPa (300 - 700 psi)
Modulus of elasticity : 14000 - 41000 MPa (2 - 6 x 106 psi)
Permeability : 1 x 10-10 cm/sec
Coefficient of thermal expansion : 10-5 oC-1 (5.5 x 10-6 oF-1)
Drying shrinkage : 4 - 8 x 10-4
Drying shrinkage of reinforced concrete : 2 - 3 x 10-4
Poisson's ratio : 0.20 - 0.21
Shear strength : 6 - 17 MPa
Specific heat capacity : 0.75 kJ/kg K (0.18 Btu/lbm oF (kcal/kg oC))
Applications
-Medical orthoses; bridges, pillars, columns, archways
Fiberglass
Structure
Properties
An individual structural glass fiber is both stiff and strong in tension and compression—that is, along its axis. Although it might be assumed that the fiber is weak in compression, it is actually only the long aspect ratio of the fiber which makes it seem so; i.e., because a typical fiber is long and narrow, it buckles easily. On the other hand, the glass fiber is weak in shear—that is, across its axis. Therefore, if a collection of fibers can be arranged permanently in a preferred direction within a material, and if they can be prevented from buckling in compression, the material will be preferentially strong in that direction.
Furthermore, by laying multiple layers of fiber on top of one another, with each layer oriented in various preferred directions, the material's overall stiffness and strength can be efficiently controlled. In fiberglass, it is the plastic matrix which permanently constrains the structural glass fibers to directions chosen by the designer. With chopped strand mat, this directionality is essentially an entire two dimensional plane; with woven fabrics or unidirectional layers, directionality of stiffness and strength can be more precisely controlled within the plane.
A fiberglass component is typically of a thin "shell" construction, sometimes filled on the inside with structural foam, as in the case of surfboards. The component may be of nearly arbitrary shape, limited only by the complexity and tolerances of the mold used for manufacturing the shell.
The mechanical functionality of materials is heavily relied on the combined performances of the both resin (AKA matrix) and fibres. For example, in sever temperature condition (over 180 °C) resin component of the composite may lose its functionality partially because of bond deterioration of resin and fibre. However, GFRPs can show still significant residual strength after experiencing high temperature (200 °C).
Applications
-Storage tanks, house building, piping
Carbon-fiber-reinforced composite
Also called:
-carbon-fiber–reinforced plastic
-carbon-fiber–reinforced thermoplastic
-carbon fiber
Structure
Properties
Carbon-fiber-reinforced composites consist of two parts: a matrix and a reinforcement. In CFRP the reinforcement is carbon fiber, which provides the strength. The matrix is usually a polymer resin, such as epoxy, to bind the reinforcements together. Because CFRP consists of two distinct elements, the material properties depend on these two elements.
The reinforcement will give the CFRP its strength and rigidity; measured by stress and elastic modulus respectively. Unlike isotropic materials like steel and aluminum, CFRP has directional strength properties. The properties of CFRP depend on the layouts of the carbon fiber and the proportion of the carbon fibers relative to the polymer. The two different equations governing the net elastic modulus of composite materials using the properties of the carbon fibers and the polymer matrix can also be applied to carbon fiber reinforced plastics. The following equation,
is valid for composite materials with the fibers oriented in the direction of the applied load. 
is the total composite modulus, 
and 
are the volume fractions of the matrix and fiber respectively in the composite, and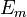 
and 
are the elastic moduli of the matrix and fibers respectively. The other extreme case of the elastic modulus of the composite with the fibers oriented transverse to the applied load can be found using the following equation:
The fracture toughness of carbon fiber reinforced plastics is governed by the following mechanisms: 1) debonding between the carbon fiber and polymer matrix, 2) fiber pull-out, and 3) delamination between the CFRP sheets. Typical epoxy-based CFRPs exhibit virtually no plasticity, with less than 0.5% strain to failure. Although CFRPs with epoxy have high strength and elastic modulus, the brittle fracture mechanics present unique challenges to engineers in failure detection since failure occurs catastrophically. As such, recent efforts to toughen CFRPs include modifying the existing epoxy material and finding alternative polymer matrix. One such material with high promise is PEEK, which exhibits an order of magnitude greater toughness with similar elastic modulus and strength. However, PEEK is much more difficult to process and more expensive.
Despite its high initial strength-to-weight ratio, a design limitation of CFRP is its lack of a definable fatigue endurance limit. This means, theoretically, that stress cycle failure cannot be ruled out. While steel and many other structural metals and alloys do have estimable fatigue endurance limits, the complex failure modes of composites mean that the fatigue failure properties of CFRP are difficult to predict and design for. As a result, when using CFRP for critical cyclic-loading applications, engineers may need to design in considerable strength safety margins to provide suitable component reliability over its service life.
Environmental effects such as temperature and humidity can have profound effects on the polymer-based composites, including most CFRPs. While CFRPs demonstrate excellent corrosion resistance, the effect of moisture at wide ranges of temperatures can lead to degradation of the mechanical properties of CFRPs, particularly at the matrix-fiber interface. While the carbon fibers themselves are not affected by the moisture diffusing into the material, the moisture plasticizes the polymer matrix. The epoxy matrix used for engine fan blades are designed to be impervious against jet fuel, lubrication, and rain water, and external paint on the composites parts are applied to minimize damage from ultraviolet light.
The carbon fibers can cause galvanic corrosion when CRP parts are attached to aluminum.
Applications
-Carbon fiber microelectrodes, sporting goods